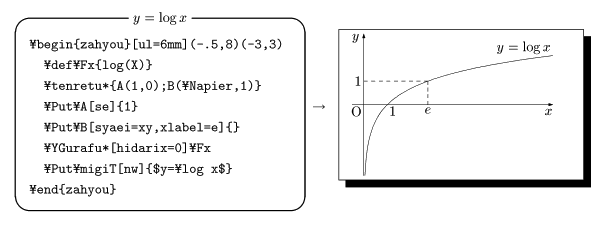
(5) y=f(x) のグラフ描画(4) 区間を限定された場合(2)

  定義域が開区間の場合でも，前回取り上げた
        y=4+3x-x^2 (0<x<4)
の場合には，端点 x=0, 4 において，y の値は計算可能です。
  それに対して，
        y=log(x) (x>0)
では，端点 x=0 において，log(0) は定義されていません。
したがｔって
        YGurafu{log(X)}{0}{\xmax}
はエラーとなります。
対応法の一つは
        YGurafu{log(X)}{0.01}{\xmax}
などと，端点 0 を避けることです。
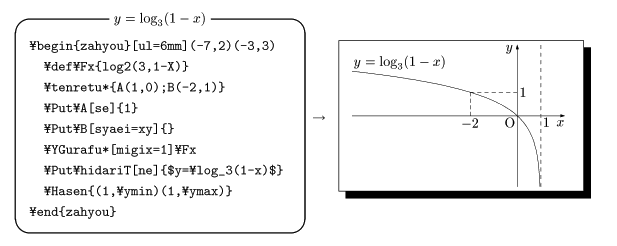
もう一つの対応法は
        \Gurafu*[hidarix=0]{log(X)}
と，\YGurafu* にオプション引数で描画範囲を限定する方法です。
こちらが便利かと思います。

Perl の対数関数 log は自然対数です。
他の底にたいしては，emath では
        log2(底, 真数)
なる関数を用意しています。

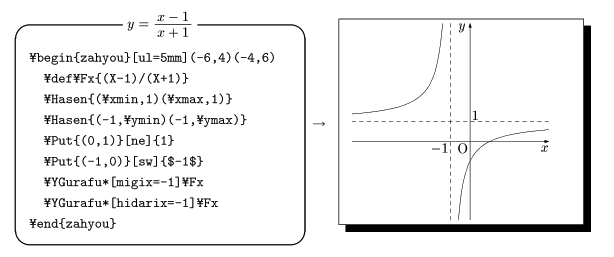
分数関数で，分母に零点がある場合は，連続な枝ごとに
        \YGurafu
を発行します。

ソースリストはこちら

【練習問題】

 つぎの関数のグラフを描画せよ。（私の作例））
    (a) y=1/x^2
    (b) y=x^2/(x-1)
    (c) y=log(|x|)
    (d) y=x*log(x)